Chapter 5:
Simulating Protein Self-Assembly
Sic parvis componere magna solebam
(In this manner I was accustomed to compare great things to small.)
________________________________- Vergil
Index |
Last Chapter |
Next Chapter |
Sic parvis componere magna solebam
(In this manner I was accustomed to compare great things to small.)
________________________________- Vergil
There are many dynamic systems within the cell, and in other small-scale systems, that are difficult to fully understand, and hard to study using conventional experimental analysis. The exact method by which proteins of the cytoskeleton combine, the way that viruses assemble out of their component proteins, and the general interaction of proteins and other macromolecules are all difficult to determine by observation alone.
Direct inspection of living tissue is usually unable to resolve these interactions, except in aggregate form, while higher magnification methods generally work only on specially prepared tissue. The processing needed to prepare specimens for most high magnification techniques, such as electron microscopy, usually kills and immobilises the tissue, halting any dynamic processes. While some preparatory techniques such as rapid freezing may preserve a snapshot of a dynamic process, it is still often difficult to determine the full process, although such frozen specimens can provide useful data about such dynamic processes. (1)
Indirect methods can, however, be very useful. Techniques such as protein sequencing and X-ray crystallography can reveal the shapes of proteins, and these and other techniques can be used to determine what areas of the protein are active and can bind to other molecules. They and may even suggest how a protein may change its conformation, and under what conditions. Other methods, such as analysing reaction rates and deducing early states, can also be very useful, as will be shown below.
Despite all these methods, however, it can still be difficult to establish the combinatorial nature of macromolecular interactions at the nanometre scale. Even if the initial conditions and the end result are known, the manner by which the reaction proceeded may still be uncertain. Establishing this method can reveal many interesting things about how structures at this scale function.
The most successful method for studying dynamic processes so far has been mathematical analysis of experimental results. Using observations of bulk properties such as gross polymerisation rates, a surprising amount of detail can be inferred.
Fumio Oosawa was a pioneer of this approach. Using a simple mathematical model of polymerisation similar to that used in polymer chemistry, he and his co-workers were able to accurately model the assembly of a number of self-assembling proteins. Much of their work concentrated on actin and bacterial flagella, but they also reproduced a variety of other, less easily modelled, self-assembling protein structures. (2)
The Oosawa model, in essence, treats the growth rate of a polymer as being independent of its length, once the polymer is larger than a certain critical size, known as the 'stable nucleus' size. For a polymer larger than this size, the growth of the polymer can be expressed as a combination of a growth rate, multiplied by the concentration of 'available' free monomers that can be bound, minus the disassociation rate (or loss rate) of bound monomers breaking away from the polymer.
For a given polymer of sufficient size, the growth rate G is
G = 
(5.1)
where
k + = the binding rate of free monomers to the polymer
k -- = the loss rate of bound monomers from the polymer
c1 = the concentration of free monomers to be bound
Applied to a single polymer, the above equation must be interpreted in terms of probabilities, since the binding and loss rates are only accurate in aggregate. However, this equation can be used to provide a description of the change in the population of all polymers with sub-units of size i, and hence a description of the population of all polymers; (3)
(5.2)
where
ci = the concentration of polymers of size 'i' sub units
t = time
k+ = the binding rate of free monomers to the polymer
k -- = the loss rate of bound monomers from the polymer
c1 = the concentration of free monomers to be bound
This equation tells us that the number of polymers of a particular size i subunits
Since the rate constants are assumed under this model to be independent of polymer size, they are constant for all size i > nucleus.
A similar equation is used to describe the production of nuclei, that is polymers of critical size io , that are assumed to have different 'on' and 'off' rates:
(5.3)
where, in addition to the variables described above,
k*+ = the creation rate of nuclei from free monomers
k*- = the destruction rate of nuclei to free monomers
By fitting these two equations with experimentally observed 'on' and 'off' rates k, (and by deriving further results) it is possible to match the experimentally observed behaviour of some protein species' polymerisation, reproducing details such as the bulk polymerisation over time and the steady-state size distribution of polymers.
Unfortunately, the techniques used by Oosawa for actin and other polymers do not work so well when applied to more complex polymers, such as tubulin or viral capsids. The Oosawa model makes a number of assumptions that are not universally valid.
These limitations are often not a concern, because for many proteins the Oosawa model produces accurate results, implying that the above assumptions are, for that particular case, valid.
More elaborate methods generalising the approach taken by Oosawa can be used to tackle more complex systems, and produce more accurate results. For example, by extending Oosawa's equations to cover two stages of nucleus assembly, (4) or multiple intermediate stages of assembly (5), the formation of microtubules can be more closely modelled.
While such methods give increasingly accurate results, there is still a degree of approximation involved, because the mathematical models must still make a number of simplifying assumptions. Usually the same assumptions as the Oosawa model are made (single monomer addition, constant 'k' rates, no helper proteins, a single protein species, and a homogenous environment), with a more detailed handling of the nucleation process being the primary change. Even this single change can result in complex series of simultaneous non-linear equations being generated. (6)
For some systems, useful results can be obtained using "rule based" systems, where each protein assembles into a structure dependant on simple positional rules, which adjust the type and angle of bonds. Such a simulation has been used effectively by Berger et al. to study viral capsid assembly (7). Rule based simulations can give important insights into structural assembly, as well as incorrect assembly, of complex protein structures.
This type of simulation is not, in its simplest form, a dynamic simulation, but is almost entirely mathematical in nature. It can however form a useful basis for more elaborate simulations, as described later in this thesis.
In order to better understand the structure and dynamics of a number of these self-assembling complexes, and to overcome some of the limitations of traditional mathematical analysis, it is useful to simulate on a computer the motion and behaviour of self-assembling particles such as proteins.
Of course, this is in fact simply the creation of yet another even more complex mathematical model. But, by expressing our model as a series of computer algorithms, the dynamic system can be modelled in far more detail, in three dimensions, with the aim of capturing all the significant details of the physical processes involved. If the computer model is sufficient, and correctly simulates these processes, it should produce more accurate simulated results (in comparison to experiment) than the simpler mathematical models, and should be able to make predictions about the behaviour of new systems.
In addition, computer simulation allows the relaxation of all of the above mentioned constraints. Multiple-monomer addition and differentiated addition and subtraction k rates can be modelled, as can complex interactions between multiple protein species.
The shortcomings of a computer based approach are that it does not yield analytical solutions in the way that a traditional mathematical model does, and the simulation may require so much input data that its predictive power is compromised.
However, a computer simulation can provide far more information than a traditional mathematical model. A computer model can be used to study details of processes missing in other models. Considering just the process by which tubulin assembles to form microtubules (tubulin being a protein whose behaviour is not fully described by the Oosawa model), researchers have used simulation to study a number of features of this process, such as the addition and subtraction processes occurring at a microtubule growth tip, (8) and the growth and cyclic behaviour of microtubule populations (9), (10).
While attempting to model the dynamics of just one such self-assembling protein, tubulin, it became apparent that a generic simulation program dealing with small objects of nanometre scale in solution would be desirable. Indeed, such a simulation, if sufficiently flexible, could be extended to study otherwise static structures involved with dynamic objects (such as the flow of molecules through plant plasmodesmata, or the deposition of stain particles on an electron microscope specimen).
In order to better understand how these and other proteins combine, a generic computer model to simulate their interactions is needed. By comparing the results of this computer model with experimental data, the gross accuracy of the model can be established. While comparable large-scale results do not prove that the model is accurately simulating the fine-scale detail of the molecular interactions, it does provide supporting evidence. By attempting to make the details of the model as physically accurate as possible (and checking that, even in the absence of chemical interactions, the simulator correctly models the basic laws of physical chemistry) further credibility is added to the simulator's portrayal of the dynamics of nano-scale self-assembly.
The resulting program, dubbed the 'nanoscale simulator', (or 'nanosim' for short) has grown from its original roots as a simulator for a single type of protein, tubulin, and now covers a wide range of nanoscale objects. It is able to model multiple different types of objects (each with their own specific movement and interactive properties), interacting in the same environment. It also models a variety of different states for each individual object - for example whether the object is phosphorylated or not - and defines a set of events for each object that may change that state.
In addition to proving useful in the study of the cytoskeletal and cytoskeleton-related proteinaceous structures originally aimed for, the nanoscale simulator may have a much wider application. There are many other biological self-assembling systems of interest, and it is even conceivable that the simulator would be of value for inorganic systems, such as the micro-machines envisaged by the proponents of nanotechnology (11).
By allowing us to simulate the behaviour of new systems, the nanosimulator may also have immediate practical benefits. For example, the behaviour of a new, sub-stoichiometric drug that binds to a particular protein in the growing structure to disrupt the assembly process, might be readily modelled. This may be a handy adjunct or precursor to normal biochemical analysis.
Many anti-cancer drugs, for example, disrupt the cytoskeleton (and hence cell division),to affect rapidly dividing cells such as cancer cells. They do this in very small quantities, presumably by adding defects to the growing cytoskeletal structures, which either renders them incapable of further growth, or encourages their disassembly. Similarly, some anti-viral drugs operate by interfering with the self assembly (or even disassembly (12)) of the viral coat by its constituent protein capsids.
The program will be described in detail in later chapters, along with several significant results. In this chapter details of the physical chemistry that the simulator will be required to model are given, setting the stage for a later, more detailed discussion of programming in Chapter 6.
The program simulates the movement, interaction and behaviour of objects of roughly 1 nanometre to 100 nanometres in size, moving in solution, over time periods of microseconds to seconds.
The scale of this simulator falls between those of the very, very small-scale simulators that deal with individual atoms (which operate on the scale of picometres and femtoseconds) and of traditional mechanics programs (which model 'real world', mechanical objects on scales of millimetres and metres, and work on the order of seconds or minutes).
The main thrust of the simulator is examining self-assembling objects, and simple forms of 'emergent behaviour' that occur when simple rules applying to low level structural components have significant resultant effects on the high level structures they compose. By modelling individual large molecules it is hoped to derive useful higher-order results, such as the behaviour of the large-scale aggregates they may form.
In order to model the behaviour of these large molecules, the behaviour of the smaller solvent molecules must also be implicitly modelled. General rules for the physics of simulated objects must be defined such that the same rules can be used both for free objects and for objects that have collected together into aggregates.
The simulator does this by modelling the basic physics of the environment. Since to do this completely accurately is computationally infeasible, a number of assumptions and simplifications are made about the way molecules interact with their environment. In this way an abstracted, but manageable, model of the system to be simulated is used.
The simulator models mixed solutions of different types of molecules. Normally the simulator starts with an unstructured environment, with all the components randomly distributed throughout the simulation space. However it is also capable of starting with a more ordered environment (read in from a file), such as one containing a pre-existing aggregate or indeed a large-scale proteinaceous structure (such as a modelled plasmodesmata).
Using the physical model and the description of the objects it is given, the simulator examines how molecules at this nano-scale level interact, and particularly how large-scale aggregates form and change. The main work that the simulator has been used for so far is looking at actin and tubulin, and the filaments and microtubules they build up. But it has also been used for a number of other purposes, such as modelling the deposition of stain particles on a sample for electron microscopy, and preliminary work on viral self-assembly.
Recent work published by Schwartz et al. follows a similar general path (13). R. Schwartz, P.W.Shor, P.E.Prevelige Jr., and B. Berger extend the earlier work on rule-based systems of Berger et al., combining it with a kinetic simulator to perform a general 3-D simulation of viral capsid assembly. The rule-based kinetic model uses a sophisticated representation of bonds with lengths, directions, rotation vectors, association and dissociation activation energies, spring constants for bound molecule interactions, allowable neighbours and tolerances. This model also uses a rule-based system for protein conformational change.
A number of these attributes, specifically the variation in bond angles and the activation energy based binding/unbinding rules, are not covered in the model presented in this thesis. The computational load involved in modelling these features is, according to the authors, very great, and limits the number of particles that can be simulated within a reasonable time to a few hundred (on an 8-processor Sun Ultra Enterprise 5000 symmetric multiprocessor), but provides an insight into the dynamics within the assembled structure, which is lacking in this thesis.
The model presented is very powerful, and there is no reason to suppose that it cannot be extended to handle its current (apparent) limitations:
This "rules based simulation" does have a number of advantages over the work presented in this thesis, especially in its detailed model of the intra-aggregate behaviour of proteins in the assembled aggregate. Inter protein bonds are represented as having a characteristic angle and length, with translational, rotational and bending forces pushing the bond towards its "ideal" position. This makes the bound proteins dynamic, and allows for investigation of "incorrect" bindings, where a complex structure (such as a virus shell) assembles incorrectly because of a protein binding in an incorrect position due to cumulative error caused by the bound units not being in their "ideal" positions (14).
The simulator models the physical environment of objects (usually proteins) moving in a solvent. Since the scale of the simulation is well above the femtosecond level of individual atoms, it does not attempt to model the direct velocities and forces involved at the lowest level. Similarly, interactions between objects are not made at a low, atomic level. Rather, potential "binding sites" for the modelled proteins are identified, and a probabilistic method determines whether binding occurs.
The simulator works in a series of repeated time steps, or "program cycles". A single program cycle might model a period of ten microseconds, during which particles will move, collide, and perhaps bind with others. After each cycle some form of data output may occur, and then the next cycle is run.
The program is thus required to accurately model:
In the following sections the details of the physical chemistry required for each of these steps will be examined.
The objects/proteins are modelled as moving in a continuous sea of solvent. The objects modelled are usually much larger (perhaps 10,000 times) than the solvent particles around them, and over the course of even one program cycle, will usually interact with many millions of solvent particles.
A fundamental question for our modelling is at what level of accuracy should these molecules be simulated. A complete solution would try to model everything, but of course this is always going to be impractical. The problem is to know where to stop - should the model work at the molecular, the atomic, or even the subatomic level? What level of accuracy is sufficient? The answer is likely to be determined by what level is practicable (i.e. how big the computer is) and what level is absolutely necessary (i.e. at what stage of approximation do the results become meaningless). If these two requirements do not overlap, it may be found that the problem cannot be modelled at all.
One approach, as described in Chapter 3, is to model all the molecules in a liquid. The velocities can be calculated for every molecule, and the collisions of every molecule modelled in the same way as is sometimes done when simulating a gas. In a liquid, however, the closer spacing of the molecules causes their continuous interaction through Van der Waals' forces. (15) This continuous interaction causes the molecules to follow more complex, non-linear paths, so this is not an accurate method. However, such a simulation can be done in time steps that are smaller than the average time between collisions, and these more complex paths approximated.
Since the same closer spacing of molecules leads to far more molecular collisions occurring over a given time within a given space, this requirement for small time steps places a great computational load on such a model, which can nonetheless be used to simulate small quantities of liquid, and thus derive various liquid properties. (16)
A similar approach is to model every molecule and perturb them randomly, working out their final positions as probabilistic functions of the potential energy in the local region of each molecule, also described in Chapter 3. (17)
At the scale of the simulations in this thesis, where thousands of self-assembling proteins are simulated, each of which is usually 10kD+ in size, to do this is completely infeasible. For example, a simulation of 10,000 40kD proteins, even at a reasonably high concentration, would still involve on the order of 10,000,000 solvent molecules. As a further complication, the simulation would have to be carried out in steps on the order of picoseconds, whereas many of the results of interest involve polymerisation over entire minutes. Obviously, if a way can be found to deal only with large protein molecules, and on a time scale of microseconds, the complexity of the problem can be reduced by up to twelve orders of magnitude.
Fortunately, it is not to difficult to do this. As outlined in Chapter 3, when a molecule in solution is much larger than the solvent molecules, its motion can be treated as a random walk within a continuous fluid. A random walk is simply the path taken by a particle when it has a great many random collisions. If these collisions are frequent enough they can, paradoxically, be ignored on an individual basis, and simply treated as an aggregate effect, since a particle undergoing a random walk tends to move in a Gaussian manner. That is, the probability of finding the particle at any given point is given by a normal curve: it is most likely to be found at its origin, and is approximately 65% likely to be found within one standard deviation of that origin.
In order to find the rules governing the motion of a single molecule, the large-scale (and measurable) properties of molecules in aggregate must be considered, in order to discover the exact form of the probabilistic normal curve governing the movement of the molecule.
The diffusion equation describes the macroscopic properties of a solution, specifically that the concentration of a solution changes over time in proportion to the second derivative of the concentration gradient. This is to some extent intuitive: particles are expected to move from areas of high concentration to areas of low concentration, a process that acts, over time, to 'smooth over' initial irregularities in concentration .
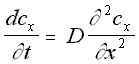One-Dimensional Diffusion Equation (5.4)
D = Diffusion constant of molecule
cx = concentration (in x-direction)
To illustrate, consider a solvent in a volume where, at t=0, all of the solute is on the plane x=0. (e.g. a bucket with solute molecules on the bottom, into which the solvent is poured at t=0, shown in Fig. 5.1.)
The general solution to a second order partial differential equation of the type above is:
Solution to One-Dimensional Diffusion Equation
(5.5)
cx = concentration (in x-direction)
D = Diffusion constant of molecule
k = a constant
Specifying the boundary conditions enables us to determine k. If the total number of solute particles is N, then k can be found by integrating the above expression for concentration (in the x-direction) over all "x" for a suitable t (this is allowable, since the number of solute particles is constant over all t). By then taking t = 1/D, the following convenient expression is found:
Concentration Gradient at time t = 1/D (5.6)
Integrating this concentration function from x=0 to x=infinity gives:
Solution for Constant in Diffusion Equation (5.7)
Thus, given the boundary conditions that all N particles at t=0 start at x=0, the one-dimensional diffusion equation gives the resulting concentration gradient for any positive time t as:
1-D Concentration Gradient Solution (5.8)
The general form of this equation can be kept, but expanded to three dimensions, by postulating a cross-sectional area A. This gives the 'bucket' a specific radius, and allows the volumetric concentration to be found by simply dividing the above by area. The concentration is assumed to be constant for any given x, varying only in the x direction. This gives the final form of the concentration function as:
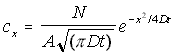Linear 3-D Concentration Gradient (5.9)
cx = "true" 3-D concentration in the x direction
N = the total number of particles
A = the cross-sectional area of the container
D = the diffusion constant
Care is needed when considering the motion of a diffusing particle, since it is a random walk. What is of primary interest is the average distance travelled over a period of time t, the 'mean displacement'.
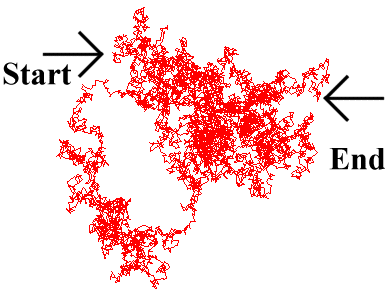This is different from the actual distance covered by the particle. Furthermore, the instantaneous velocity
of the particle may be much greater than would appear from this 'mean displacement', as the particle
bounces continuously from solvent molecule to solvent molecule. This is due to the fractal nature of
Brownian motion, where the particle moves over a much greater distance than would be imagined merely
by observing its start and end point over a period of time, as it continually backtracks and sidesteps,
bouncing around at random (Fig. 5.2).
The mean distance travelled by a solute particle can be found by expanding the previous result. At t=0, all the particles are at x=0. At any later time, they are found spread over the entire range of 0 to x . Hence, the mean distance travelled by all the particles from t=0 to some new time t=T is simply the weighted sum of the concentration gradient. Considering the x-direction only, and using the one-dimensional concentration gradient:
(Eqn 5.8 repeated)
if cx × x/N is integrated to find the weighted sum, this results in the mean distance travelled by all particles, and hence the average distance travelled by any given particle (from time t=0 to a new time T). This gives:
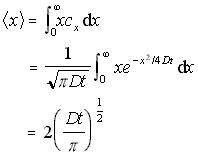Mean 1D distance travelled (5.10)
The mean square distance
In a similar fashion, the one-dimensional mean square distance travelled can be found by integrating x2cx /N. This is useful, as it can be generalised to the case where particles are diffusing in both directions from the origin.
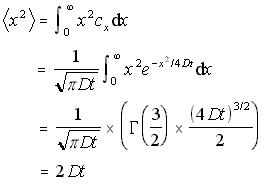1D Mean Square Distance (5.11)
This simple result is quite unsurprising: in actual fact it could have been
read directly from the concentration function above, by making the substitution
t2=x2/2-Dt and comparing the result with the
standard form of the normal curve:
.
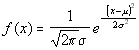Eqn. 5.11 gives a solution,
but only for motion in one co-ordinate. To find the general formula for motion
in all three dimensions, the
concentration gradient given by an initial point source (say a pellet of
solute dropped into a bucket) can be considered (Fig.5.3).
At t=0, all N particles are at the origin (x=0,y=0,z=0). After this time, the particles spread throughout the entire space. As before, the solution to the diffusion equation given these boundary conditions is required.
The diffusion equation in three dimensions is:
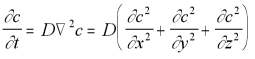3-D Diffusion Equation (5.12)
However, given the geometry of the situation, it will be better to give this in spherical polar co-ordinates, which gives the rather more complex-appearing equation:
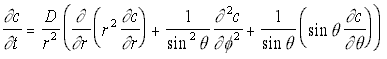3-D Polar Diffusion Eq. (5.13)
However, because our concentration is expected to have spherical symmetry only the distance from the origin will matter, not the angle, so this can be simplified to:
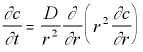3-D Polar Diffusion Eq. with Radial Symmetry (5.14)
The general solution to this spherical diffusion equation is:
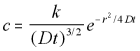3-D Radial Polar Diffusion Equation General Solution (5.15)
k = a constant
D = diffusion constant
r = radial distance from origin
t = time
To find the exact form of the equation, for a concentration of N particles, the procedure outlined above can be repeated. By choosing t = 1/D, the concentration
gradient is obtained in the simplified form 
. Integrating this over the entire volume, k is found as:
Solution for 'k' Constant for Eq.(5.15)
This gives the final form for the three-dimensional concentration function for the boundary conditions that at t=0, x=0 for all N particles:
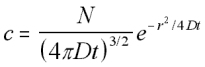3-D Radially Symmetric Concentration function (5.16)
Now that the concentration function for a spherical concentration is defined, the mean square distance can be found in the same manner as above, by integrating x2c/N over the volume.
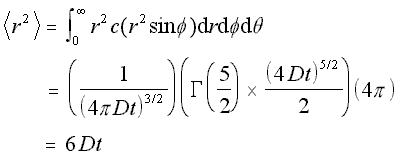
Mean Square Distance for Radial Concentration (5.17)
This is expected, since it is three times the mean square distance obtained earlier for the linear case. Hence the root mean square value, or standard deviation, of the motion in the 3-D case is the square root of three times the standard deviation in the linear case, which is what would be found by simple addition of vectors.
All these formulas rely on the Gaussian formula being an adequate approximation to the real random walk nature of the molecular movement. For the approximation to be valid, the times and distances between collisions of the solute particle with the solvent particles must be substantially less than the times and distances being used in our simulation.
The Einstein-Smoluchowski equation (18) provides a handy check that this is the case:
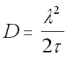Einstein-Smoluchowski Equation
lamda = the length of the average "jump" between collisions
tau = the average time difference between collisions
It is reasonable to assume that the average distance between collisions will be on the order of the size of a water molecule (say, around 250pm). In this case, for a very small protein with a diffusion constant of D = 1 x 10-10, the value of will be 312ps.
Hence, so long as the simulation operates on the order of milli- or micro- seconds, it is reasonable to expect that the particle will undergo thousands or millions of solvent collisions for each simulation step, and the Gaussian approximation will be valid.
If the diffusion constant is known for a solute in a given solvent, the initial concentration profile of that solute, and the boundary conditions of the vessel enclosing the solute, the concentration gradient function for all time can be found using the diffusion equation.
Similarly, while considering a single particle, a probability distribution for possible positions in the particle's future can be determined from the same information . While the particle moves in a Brownian (or 'random walk') manner, at a time t in the future the probability of the particle being found at a given point is given by a Gaussian probability function, with a variance of 2-Dt in each of the x,y,z co-ordinates, unless this is modified by boundary conditions.
This gives the standard deviation for a molecule's motion (the root mean square of the expected change in position over a time period 't') as being, in polar co-ordinates:
RMS radial change in position (5.18)
- The actual angle from the origin is entirely random.
Expressing these results in a different way, the standard deviation in linear co-ordinates can be written, where it is simply:
RMS Displacement from the Diffusion Eqn. (5.19)
Modelling all this activity is infeasible on current (2000) equipment, and is in any case unnecessary. The outcome of such a large number of interactions of a large particle with many solvent particles is well known, and is the famous 'random walk' of Brownian motion. (19)
In the previous section, it was shown how a particle's diffusion constant can be used to determine its mobility. The diffusion constant of small, agile molecules has a greater numerical value than that of a large, slow-moving macromolecule. The diffusion constant provides an easy way of calculating the RMS distance travelled by molecules over a given period of time.
These diffusion constants can be most accurately obtained by laboratory measurement. There are a number of methods used to do this, such as the capillary and the diaphragm techniques (20). In the capillary technique a solute-filled capillary tube is dipped into a larger container of solvent, and the outflow of solute molecules is measured by monitoring the concentration in the capillary. The diaphragm technique works in a fundamentally similar fashion.
For the nanoscale simulator however, the situation is more complicated. While it is possible that the diffusion constant will be known for the free monomer, the diffusion constant varies with the size of the diffusing object, and it is unlikely that it will be known for the various sizes of polymer that the monomers form. But when the diffusion constant cannot be directly measured, a reasonably accurate theoretical approximation can be resorted to.
The Stokes-Einstein equation describes the way that diffusion increases in proportion to temperature, and is inversely proportional to the frictional force experienced by a molecule:
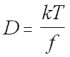Stokes-Einstein Equation (5.20)
D = diffusion constant
k = Boltzmann constant
T = temperature
f = frictional constant
As both the Boltzmann constant and the temperature are known, all that is required to determine the diffusion constant is to find the frictional constant f. Determining this exactly is again a matter for experimentation, but it can also be determined reasonably accurately on theoretical grounds for various polymer shapes and weights.
Stokes' relation gives us a theoretical value for the frictional co-efficient of a spherical particle in a solvent:
Stokes' Relation (5.21)
r = particle radius
= solvent viscosity
The difficulty here (and where inaccuracy arises) is that the particle radius is not simply the physical radius of the molecule, but is rather the effective radius of the molecule, taking into account the effects of solvation (solvation is the layer of ordered water that the electric field of a protein causes to form around the protein). Also, the formula is strictly only accurate only for a single spherical particle. It can be modified easily to take account of prolate and oblate ellipsoids, but even these, like the sphere, are usually only approximations to the true shape of the particles.
The following formulas give the theoretical frictional constants for different shaped proteins, and are used by the nanosimulator to generate theoretical values when experimental values are unknown.
Sphere(5.22)
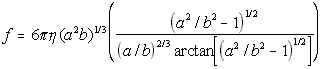
Oblate Ellipsoid(5.23)
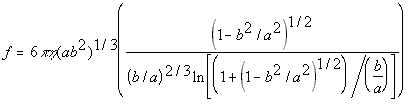
Prolate Ellipsoid(5.24)
where
eta = solvent viscosity
r = particle radius
a = half major axis
b = half minor axis
While the nanoscale simulator allows users to directly input the diffusion constant of their molecule, if known, it will also try to calculate a value using formulas 5.22,5.23 and 5.24 if the diffusion constant is unknown.
This is straightforward if there is only a single spherical particle being modelled, for which the Stokes' relation, as given above, can be used. However, frequently it is necessary to model molecules that are not even approximately spherical, in which case the simulator allows the entry of multiple spheres to represent the desired structure.
Unfortunately, a set of multiple spheres, whether describing a single monomer, or a series of monomers combined into a polymer, is neither a prolate nor an oblate ellipsoid, so approximation is required. (It would be possible to numerically simulate the frictional coefficient of a set of spheres, or even that of the "true" molecular shape, but that is beyond the scope of this thesis.)
An approximation that seems to work reasonably well for the purpose of diffusivity calculation and is easy to implement, is to represent the monomer or polymer, by an ellipsoid that has the same moments of inertia as the set of spheres used by the model. This works well for symmetrical arrangements, and less well for non-symmetrical ones. The moments of inertia (MOIs) are automatically calculated by the simulator when the molecular model is read in, or when a polymer is created, and compared against the general formula for the moment of inertia of an ellipsoid:
Ellipsoid Moment of Inertia (5.25)
where a specific MOI is taken along a given semi-axis, M is mass, and a and b are the perpendicular semi-axes. (A semi-axis is half of either the major axis or a minor axis).
The model calculates the effective values of the major and minor axes from the pre-calculated MOI by reversing this formula, and then proceeds to calculate the frictional constant based on these figures, using eqn 5.22, 5.23 or 5.24 as appropriate. It may also optionally add a small, user-defined, amount to the effective size of the molecule, to represent the effect of solvation.
1. A small molecule
Consider the molecule SO42-.
It is approximately spherical and has an approximate hydro-dynamic radius
210 pm = 210 × 10-12 m. The Viscosity of water = 0.891 x 10-3 kg m-1 s-1 (at 300K)
Stokes' equation gives a frictional coefficient:
f = 6 x 3.14159 x (210 x 10-12) x (0.891 x 10-3)
= 3.527 x 10-12 kg s-1
Using the Boltzmann constant, k = 1.38 x 10-23
and T = 300 K, the Stokes-Einstein equation gives us:
D = kT/f
= ( 1.38 x 10-23 ) x ( 300 ) / 3.527 x 10-12
= 1.16 x 10-9 m2 s-1
This compares well with the experimentally determined value (24) of 1.10 x 10-9 m2 s-1.
For illustrative purposes only, consider the 68kD protein haemoglobin as being a sphere of radius 3.5nm.
Stokes' equation would gives a frictional coefficient of f = 5.88 x 10-11 kg s-1.
The Stokes-Einstein equation would then predict a diffusion constant of D = 7.0 × 10-11 m2 s-1, which compares well with the experimentally determined value (25) of D = 6.9 x 10-11 m2 s-1 .
By using Stokes' relation (5.21) and the Stokes-Einstein equation (5.20), and by approximating the shape of monomers and polymers when experimental diffusion constants are not known, theoretically calculated diffusion constants can be determined, allowing the nanosimulator to approximate the diffusive movement of simulated particles.
The Brownian motion of individual particles causes the diffusive behaviour of mixed liquids. Using the diffusion constant D, the change in position of a particle after a time t is found to be probabilistically distributed over a normal curve, with standard deviation:
RMS Change in Cartesian Co-ordinates (Eq. 5.19)
This allows the full characterisation of Brownian motion. It also allows the modelling of the very first aspect of a particle's behaviour: where it will move after a single time step.
When the program simulates the movement of an object, either a monomer or a polymer, it uses a Gaussian function for each of the x, y and z directions, with the standard deviations defined above, to determine where the object will appear after the next time step.
Another aspect of movement to consider is that of rotation. For small particles moving large distances in comparison to their size, it can be assumed that their final orientation is essentially random. They will have been involved in so many collisions that they may face in any possible direction after a time step.
For larger objects, especially large polymers, the situation is not so simple. An entire microtubule, for instance, does not rotate randomly over the course of a microsecond.
The simulator handles this problem by calculating the moment of inertia for all objects, incrementally adjusting the moment of inertia for aggregates as objects join and break off. If the moment of inertia is sufficiently large, it calculates a non-random orientation, based on a heuristic that approximately models the rotational force the object experiences. Rotational behaviour is not strongly characterised in the simulation, but it does not need to be; as long as aggregates and objects rotate sufficiently to avoid artificial effects from unchanging orientations, the rotational behaviour should not strongly affect interactions.
The approximation used for rotational motion - which is presented without experimental proof, but which makes a useful heuristic for the simulation - is that the rotational behaviour of the object is energetically similar to the Brownian translational motion of the object (see Fig. 5.4). This is not presented as necessarily reflecting physical fact, but as a useful approximation. It is made by analogy with the quantum mechanical behaviour of much smaller molecules, where the equipartition principle (26) tells us that for a temperature sufficiently above a critical 'rotational temperature' the linear and rotational modes of a molecule will share an equal amount of the molecule's energy. Since at the scale of the simulation the quantization of these modes is so fine as to form a virtual continuum, the assumption is made that the rotational and translational energies of the simulated molecules are identically distributed.
Using this assumption that the distribution of rotational energy of the macromolecule is equal to the translational energy of the macromolecule, a further assumption is made that the Brownian nature of the translational motion can be extended to the rotational motion of the macromolecule as illustrated in figure 5.4. This implies that the rotational movement of the macromolecule, rather than being a continuous rotation with a slowly changing angular momentum, is instead a series of random changes in angular direction, caused by the irregular impact of large numbers of solvent molecules.
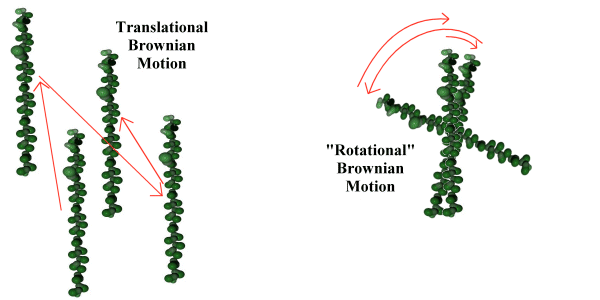Figure 5.4 Translational and rotational Brownian motion.
In order to model this, the square of the linear standard deviation for a given direction (remember that equation 5.19 states that this is equal in the x, y and z directions) is multiplied by the mass of the macromolecule, and the result equated to the angular standard deviation times the appropriate principal moments of inertia.
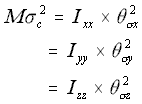The Rotational Approximation (5.26)
where
M = the mass of the molecule
c = the linear standard deviation in each of the x, y and z directions
Icc = the three principal moments of inertia
c = the angular standard deviation around the three principal moments of inertia
The above approximation is derived from classical considerations; if the object were moving with a constant linear velocity v and angular velocity , its translational energy would be:
translational energy: 
eqn (5.27)
while its rotational energy is: 
eqn (5.28)
Since in the simulation the linear displacement per unit time (corresponding conceptually to the v term above), is normally distributed with standard deviation c, the angular displacement standard deviation c , is similarly treated as corresponding to . Using the "Rotational Approximation" equation above (5.26) the three angular displacement standard deviations are found as:
,
,
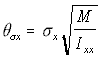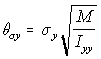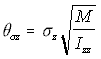Angular s.d. (5.29)
Using this approximation results in the expected behaviour: long, thin macromolecules will "roll" easily around their major axis, but will not rotate so far around their minor axes, while spherical macromolecules will move with equal ease or difficulty in different angular directions. Due to the Brownian rotational approximation heuristic, the molecules will not smoothly rotate with a fixed angular velocity, but rather will adopt new angular positions varying from their old positions to a greater or lesser extent depending on their rotational inertia.
Although this behaviour is sufficient for the purpose of this thesis, it is emphasised again that this is a simple heuristic approximation, and should not be taken as an accurate simulation of the rotational motion of large molecules in a solvent.
One of the fundamental data the simulator needs to determine is whether objects have collided or not. This turns out to be more complex than might at first be thought.
Unfortunately, it is not possible to discover whether particles collide simply by moving them independently, and checking whether their positions in the simulator overlap. There are a number of reasons for this. Firstly, if the standard deviation of their movement (i.e. the average distance they will probably move in a time step) is large compared to their size, the collision probability would be greatly underestimated. Since the particles do not move in straight lines (see Fig. 5.1), two particles which may well have interacted at some stage may end up quite widely separated. Simply checking their final positions says very little about the path they took to get there.
This difficulty could be resolved if very small time steps were used, only allowing the particles to move a fraction of their own size before again checking for collisions. However this too is unsatisfactory. To completely model the Brownian motion in this way, the time step should be dropped to the same time scale as the physical collisions which drive the Brownian motion - which would force simulation at the scale of picoseconds, or less. Otherwise there would still be a certain degree of 'fuzziness' as the object moved, even if it moved only a small proportion of the object's total size, because it would be continuously jiggling as it went. However, even assuming that the simulation is modelling a 10 nanometre sphere which is allowed to move (on average) only 1 nanometre at a time, there are still difficulties.
Equation 5.19 indicates that the distance a particle moves varies as the square root of time. Thus, if it is necessary to reduce the distance moved by a factor of ten, the time step must be decreased by a factor of a hundred. This means that moving particles by a tiny amount (still an imperfect solution) would require vast amounts of computational time. For most of the systems examined in this thesis, the free monomers are moving around ten times their diameters in a time step. To reduce this to, say, one tenth of their diameters would require running the program 10,000 times longer, which would greatly reduce its value. This is an example of the 'scaling problem', which is covered in more detail below.
Fortunately, this degree of effort is not required. If the diffusion constant and the size and position of two particles are known, it is sufficient to simply find the probability of them colliding. Thus, rather than simulating every step leading to their collision, the a priori probability of a collision is used, with the simulator determining randomly if the collision actually occurs.
This probability, while difficult to determine analytically, is comparatively simple to determine using a numerical simulation. This was done by the program described in Appendix A, and a table of scale-independent probabilities was calculated. This table of raw probabilities lists the probabilities of two spheres, of given total radius, colliding at a distance expressed as a multiple of their (weighted) combined RMS movement. Using this table, the nanoscale simulation program can determine the raw collision probabilities for different particles by scaling the results to suit the actual particles it needs to simulate at any particular moment.
The scaling works in the following manner: Consider two spheres A and B, with radii RA and RB, moving with RMS displacements per cycle of A and B , at a distance d apart. In order to collide, the centres of the two spheres must approach to within RA + RB. The problem can thus be simplified to that of a single sphere, of radius R = RA + RB, colliding with a moving point. If the point is viewed from the perspective of the newly 'enlarged' sphere A, it can be seen to have an apparent RMS displacement of = (A2 + B2)½ . The problem now has only three variables; the combined radius R, and the combined RMS displacement , and the distance d. The situation is illustrated below in figure 5.5.
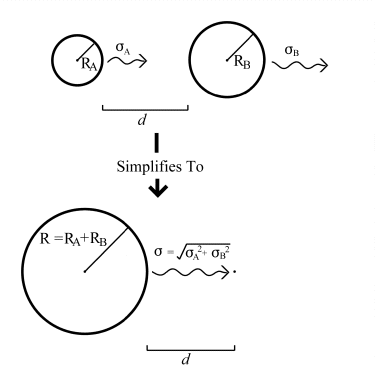
Figure 5.5.: Simplifying Collision Geometry.
Once the simulator has established that a collision has occurred, it checks to see whether binding occurs. This depends on there being available compatible binding sites on the colliding objects. If there are, and there is no physical impediment, a randomiser is used to generate a real number between 0 and 1, and this value is compared to the predetermined 'strengths' of the binding sites to see if binding occurs.
Determining these binding site 'strengths' is one of the more difficult aspects of this sort of simulation. Where possible, recourse can be made to direct experiment, but often these data have to be induced from overall reaction rates, or by examining the rate at which aggregates grow. It may be possible in future to derive many of these from the structure of the molecules involved, but this is currently very difficult (27).
A useful method that has recently been investigated by Schwartz et al. (28) is to use the theoretical probability, based on the activation energy of association Er and the activation energy of dissociation -Ed, with
probability binding =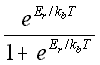 
(5.30)
probability breaking =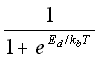 
(5.31)
kb = the Boltzmann's constant,
T = temperature
These probabilities are then evaluated if the molecules are within tolerances. This method can be extended to the simulation presented in this thesis, however the probabilities must be adjusted with respect to the time scale of the simulation. (The simulation by Schwartz et al. deliberately uses an abstract time scale. (29))
When all the movement, collision, and binding actions in a single time step have been determined, there is still work for the simulator to do. Many of the types of objects being modelled (especially the cytoskeletal proteins actin and tubulin) do not permanently polymerise - they form temporary bonds that may break. Thus, after each time step, objects that are already bound to aggregates must be checked to see whether they break away. The chance of breakage is usually derived from experimental data, and can usually be determined more easily than the chance of binding.
Many objects will be multiply bound in their aggregates however. So, rather than having a single link to the aggregate, a tubulin dimer in the middle of a microtubule may be bound to other dimers on every side. It is difficult to determine exactly how the simulator should proceed in this eventuality.
For some polymers, such as actin (and probably also tubulin (30)), it is very rare for a multiply bound monomer to break away. For such polymers, it is reasonable to set the probability for breakage of multiply bound polymers to a very low value.
One possibility is to assume that the breakage probabilities of the links are independent, and to require them to break at the same time (i.e. probability (breakage) = probability (link A breaks) multiplied by probability (link B breaks). Since the probability of a breakage is often very low, (often on the order of 0.0001 per cycle), this makes the chance of double breakages very low, and multiple (three or more link) breakages close to impossible. A shortcoming of this method is that the probabilities of these multiple breakages then become dependent on the time scale of the simulation, which is physically unreasonable.
Another option is to simply disallow multiple breakages altogether, and set their probabilities to zero. This may be appropriate for some polymers.
The solution currently implemented is to use an ad hoc heuristic, where the chance of breakages is reduced for each additional link, in some reasonable manner. The heuristic currently (optionally) used in the program is to make the probability of breakage an order of magnitude lower than the lowest breakage probability for each extra link. For example, if a monomer is bound with three links, link A having a breakage probability of 0.003, while link B = 0.002, and link C = 0.0005, the probability of breakage would be 0.0005 (the smallest) reduced by two orders of magnitude to produce a final breakage probability of 0.000005. This heuristic has the advantage of being time-independent, and still allowing multiply bound polymers to break off, albeit with a greatly reduced chance (corresponding to what some researchers observe experimentally, although this is still a subject of some debate (31), (32)).
Another solution, not currently implemented, would be to allow users to specify the breakage probabilities for all possible linkage combinations. Although this would provide the most flexibility, in all but the simplest cases it would require a considerable amount of work for the user to specify all probabilities for all possible linkages.
Possibly the best solution would be to use a more sophisticated binding model, where the linkages were treated in terms of the energy differences involved, and the association and disassociation constants derived from these numbers. This method has been used to create detailed simulations of microtubule growth tips with some success (33), as well as the recent work with virus assembly already mentioned (34).
One of the complexities of modelling biological molecules, especially proteins, is the number of different states they have. A protein may be in a high-energy or a low-energy state (often depending on whether it has been phosphorylated), it may act differently when it is bound to another protein than when it is floating free, it may even change its conformation.
What state a protein is in largely depends on its history, and its immediate environment. The simulator models this by defining a small number of 'events' that may alter the protein's status. The most obvious events are the binding of a particular site, or the breaking of a link from a particular site. A more subtle 'event' that the simulator defines is the 'random event', which can be used to model a stochastic change from an unstable intermediate state. Thus a bound protein may 'decay' from a high-energy to a low-energy state after binding.
An example of such a random event would be the process postulated in one of the theories of microtubule formation (35), when a free tri-phosphorylated tubulin dimer is bound to the growing microtubule. Under this theory, the bound dimer decays to a di-phosphorylated state after a short period of time. Another theory postulates the change almost as soon as the dimer is bound at a particular site (36).
The simulator keeps track of the state of each object, and checks whenever there is an event that may change that state. When the state changes, various other attributes of the object, such as binding and breaking strengths, may change as well.
A perennial problem with physical simulation is how to handle the boundaries of the volume it being simulated. There are two main approaches. The first is to make the boundaries an impenetrable, elastic wall, which reflects particles that attempt to move past it. The second is to use 'periodic' or 'tessellated' boundary conditions, wherein particles moving off one edge of the simulation field immediately re-enter on the other side. Geometrically, this second approach corresponds to folding the simulation space into a four-dimensional 'hyper-torus'.
The fixed, impenetrable boundary method has many computational advantages, since it avoids complexities inherent in the periodic boundary conditions. However, while it may be legitimate to use this for individual particles, where particles reflected from the wall can be thought of as corresponding to new particles entering the system while old particles leave, it fails for the larger aggregates. The difficulty is that large aggregates, which could theoretically be a substantial fraction of the size of the simulation field, will be in effect forced towards the centre of the simulation field. A further difficulty is the impossibility of an aggregate growing to a larger size than the simulation field.
Periodic boundary conditions allow for the simulation field to be effectively infinite. A particle 'perceives' an infinite, but tessellated, simulation field stretching in all directions. Without any barriers, it is free to move in any direction, as can an aggregate. Further, an aggregate can grow to a length greater than the simulation field by simply 'wrapping around' the simulation field, growing out one side and re-emerging at the other.
Periodic boundary conditions impose a larger burden on the programmer, since complex handling of interactions between particles on different edges of the simulation field must be performed. However it results in a better, less constrained model of the environment.
A difficulty for the nanoscale simulation program in using tessellated boundary conditions is that of self-interaction. A sufficiently large object (i.e. a very long actin filament) could grow to the size of the simulation field. Once this happens there is a very good chance that it will interact with itself, possibly binding head to tail to form a closed (effectively four-dimensional!) loop. In any of the simulations involving proteins such as actin or tubulin that undergo growth and decay cycles, such an object, lacking a beginning or an end (the locations where dis-assembly usually occur), would be hyper-stable, which would greatly distort the results of the simulation.
In order to avoid this, the simulation field must either be of such a size that this cannot occur (either small and lacking sufficient monomers to build such a large polymer, or large enough that the probability of a polymer that large being created can be ignored), or the results of the simulation must be monitored for signs that a polymer of this size was created. In practice a polymer of the same size, or larger, than the simulation field is rarely observed.
There is a limit imposed by computer hardware as to how many particles can (or should) be modelled, over what volume, and for how long. Ideally the 'huge' quantities used in real laboratory experiments would be used. But since a single mole of a chemical represents 6.02x1023 particles, it can be seen that this is infeasible given the cost of computer technology in 2000. In fact, it turns out that the largest number of molecules practically handled on a desktop workstation is around 100,000.
By choosing the number of particles, and choosing the molarity to simulate, the volume of the simulation is determined. For 100,000 particles at a molarity of 20 micromolar, a volume of around about 1000 nanometres cubed, or 1 cubic micrometer would be required. This represents about the largest reasonable simulation: 100,000 molecules, in a volume of 1 cubic micrometer.
Naturally this excludes solvent particles, which are assumed to be much smaller, and far more numerous, than the large solute objects. In fact, in the simulation above, on the order of 500,000,000 water molecules are included in the volume, but as explained previously they do not need to be explicitly modelled.
The simulation program runs in cycles, each of which lasts a certain amount of time, known as the time step. Therefore, in addition to the above decision, a suitable time step needs to be determined for the program. At this stage another difficulty appears, as a result of the RMS movement equation (5.19) that was derived from the diffusion equation.
The RMS movement equation describes the root mean square displacement (a measure of the average distance travelled) moved by a particle in time t in any given direction. This value is the square root of twice the diffusion constant times t.
To see how this works in practice, consider a time step of 10 milliseconds, which might at first appear reasonable. For a particular protein of around 100kD size, it may turn out that the rough scale of movement would be on the order of a micrometer in 10 milliseconds. However this is also the size of the largest practical simulation volume, and implies that all the protein particles will be moving over the entire region in every time step.
This is unacceptable for two reasons. Firstly, it would be computationally very inefficient to have to check all (100,000×100,000)/2 possible interactions of all the objects. But more importantly, it would completely defeat the purpose of simulation, which is to examine the small-scale behaviour of these proteins.
Since the RMS distance travelled decreases as the square root of the time step, the time step must be decreased. To obtain a reasonable-sized average displacement using the above example, a time step of around 1 microsecond might be necessary, which would give us an RMS distance of around 10 nanometres. At 10 nanometres, each object is likely to encounter, on average, less than one other object, which will allow for fine-scale simulation.
But this is also unsatisfactory. Many chemical reactions of interest have features that appear only over the course of entire minutes - and if 1,000,000 cycles per simulated second are required, the program will take an unacceptably long time to run.
This turns out to be a fundamental limitation of the program. It may be partially traded off by using fewer objects, but even so, the excessive number of time steps that need to be modelled make it difficult to completely simulate in vitro experiments.
By using fast algorithms and powerful computers, a reasonable simulation period and space can still be studied, but this limitation does restrict, for the time being, the range and extent of the simulation. Since computer hardware performance appears to increase exponentially over time (the observation called 'Moore's Law') this restriction should cease to be relevant comparatively soon..
In essence, the simulator treats its objects (usually proteins) as small, partially sticky balls that bounce around within a virtual liquid, occasionally colliding and binding together. The movement of these objects is governed by the laws of physical chemistry, primarily using the diffusion equation. The aggregated groups occasionally fall apart, or collide with other sticky balls, and possibly grow.
Using this simple idea (which turns out to be considerably more complex to implement - see Chapter 6) the way small particles, and in particular proteins, interact may be studied. Chapters 7 through 10 describe specific studies of systems such as the self-assembly of actin and tubulin into large structures, and the deposition of stain particles onto the samples used in electron microscopy.
Index |
Last Chapter |
Next Chapter |
1. E.g. Chrétien, D., Fuller, S.D. & Karsenti, E. (1995) Structure of Growing Microtubule Ends: Two-Dimensional Sheets Close into Tubes at Variable Rates, J. Cell. Biol., Vol 129, No 5, pp 1311-1328
2. Oosawa, F. & Asakura, S. (1975) Thermodynamics of the Polymerisation of Protein (Academic Press, New York)
3. Ibid, eqn 43 pp 48
4. Voter, W.A. & Erickson, H.P. (1984) The Kinetics of Microtubule Assembly, J. Biol. Chem., Vol 259, No 16, pp 10430-10438
5. Flyvbjerg, H., Jobs, E. & Leibler, S. (1996) Kinetics of self-assembling microtubules: An "inverse problem" in biochemistry, Proc. Natl. Acad. Sci. USA, Vol 93, pp 5975-5979
6. Ibid, pp 5978
7. Berger et al. (1994) Local rule-based theory of virus shell assembly, Proc. Natl. Acad. Sci., USA, Vol 91, pp 7732-7736
8. Tran, P.T., Joshi, P. and Salmon, E.D. (1997) How Tubulin Subunits are lost from the Shortening Ends of Microtubules, J. Struct. Bio., Vol 118, pp107-118
9. Gliksman, N.R., Skibbens, R.W. & Salmon, E.D. (1993) How the Transition Frequencies of Microtubule Dynamic Instability (Nucleation, Catastrophe, and Rescue) Regulate Microtubule Dynamics in Interphase and Mitosis: Analysis Using a Monte Carlo Computer Simulation, Mol Bio of the Cell, Vol 4, 1035-1050
10. Odde, D.J., Buettner, H.M. & Cassimeris, L. (1996) Spectral Analysis of Microtubule Assembly Dynamics, AIChE Journal, Vol 42, pp 1434-1442
11. Such devices are still speculative. Possible the best exposition occurs in popular literature such as Stephenson, N., (1996) The Diamond Age, Penguin, London
12. Badger, J et al. (1988) Proc. Natl. Acad. Sci. U.S.A. Vol 85, pp 3304-3308
13. Schwartz, R., et al. (1998), Local Rules Simulation of the Kinetics of Virus Capsid Self-Assembly, Biophysical Journal, Vol 75, pp2626-2636
14. Prevelige, P.E. Jr., (1998), Inhibiting virus-capsid assembly by altering the polymerisation pathway, Tibtech, Vol 16, pp 61-65
15. Background information on molecular motion in liquids is available in most materials science textbooks, e.g. Pascoe K.J., (1972) Properties of Materials for Electrical Engineers, (John Wiley & Sons, Chichester)
16. Atkins, P.W. (1995) op.cit. pp 832
17. ibid, pp 831
18. ibid, p855
19. E.g. Iranpour R, Chacon P (1988) Basic stochastic processes. Macmillan Publishing Company. London. Chapter 7.
20. Atkins, P.W., (1995) op.cit., pp 853-854
21. Ibid. See Chapter 23, pp 795-6, and Chapter 24, 846-856 for a more In depth treatment.
22. Ibid, p 795
23. Ibid, Appendix C26
24. Ibid, p 855
25. Tanford, C., Physical chemistry of macromolecules, Wiley, New York (1961) (cited in Atkins op.cit.)
26. See any introductory physical chemistry text, e.g. Pascoe, K.J., op. cit.
27. Janin, J., (1995), Principles of protein-protein recognition from structure to thermodynamics, Biochimie Vol 77 pp 497-505.
28. Schwartz, R., et al. (1998) op. cit.
29. Ibid, pp 2631 "It has not been possible to determine the exact mapping between time steps and physical time in terms of time-dependent phenomena such as the diffusion rate". However, while this was not necessary for Schwartz et al, there is nothing inherent in their model to suggest that it could not be done in future.
30. This can be seen by the following two papers (ref 67, 68) which, while disagreeing on the degree of stability, both agree that the microtubule wall is a fairly stable construct.
31. E.g. modeling of 'holes' in the microtubule wall in Semënov, M.V., (1996) New Concept of Microtubule Dynamics and Microtubule Motor Movement and New Model of Chromosome Movement in Mitosis, J. Theor. Biol., Vol 179, pp 91-117
32. E.g. apparent stability of microtubule wall in Waterman-Storer, C.M. and Salmon, E.D. (1998), How Microtubules Get Flourescent Speckles, Biophysical Journal, Vol 75, pp 2059-2069
33. Martin, R.S., Schilstra, M.J. and Bayley, P.M. (1993), Dynamic Instability of Microtubules: Monte Carlo Simulation and Application to Different Types of Microtubule Lattice, Biophysical Journal, Vol 65, pp 578-596
34. Schwartz, R et al. (1998) op. cit.
35. Direct structural evidence of this theory appears in Nogales, E., Whittaker, M., Milligan, R.A. and Downing, K.H. (1999) High-Resolution Model of the Microtubule, Cell, Vol 96, p86.
36. e.g. Bayley, P.M., Schilstra, M.J. and Martin, S.R. (1990), Microtubule dynamic instability: numerical simulation of microtubule transition properties using a lateral cap model, J. Cell Sci., Vol 95, pp 33-48