How the Fast Animator Works
Introduction
Modelling the appearance of objects moving at relativistic speeds
requires both the unusual colour effects,
due to relativistic and mundane doppler shifting to be modelled, and
also the geometric distortion due to the Lorenz contraction and the
finite speed of light to be modelled.
This introduction looks at how the geometry of objects appears to
an observer (or a camera), when the objects are whizzing by at
relativistic speeds.
Lorenz Contraction
The Lorenz Contraction is the well known effect whereby objects moving
swiftly in an observer's space are measured to contract in their
direction of motion. (Things get flatter when they move quick.)
This is a Real effect - if you make simultaneous measurements
of the back and front of a moving object with a stationary ruler, you
will find the length of the object has shrunk.
The contraction is given by the Lorenz contraction formula:
/---------------
contraction = \/ 1 - (V**2/C**2)
(where 'C' = speed of light,
'V' = velocity of object
'**2' = 'squared' )
Finite Speed of Light
In addition to the Lorenz contraction, if we are looking, or photographing,
an object, we can see another effect. Imagine we are looking at a long
train, travelling almost directly towards us. Light from the
headlamp at the front of the train doesn't have as far to travel as light
from the back of the train. So, light we see from the front of the train
arrives earlier - we see a more recent view of the front of the
train than the back. Since the train is travelling towards us, this more
recent view must be closer - so the train appears to be stretched...
Now, if it wasn't for the Lorenz contraction, this would mean that fast
moving objects would appear stretched and sheared - but the
Lorenz contraction almost exactly balances out this effect - the shrinking
and the stretching/shearing combine to look like the object is turning
away from us (look at the buildings in the picture gallery).
In addition to the turning however, there is a non-linear shear for objects
not an infinite distance away.
Modelling the Shape of Objects
The upshot of all this is that if we wish to find where an object
appears to be to an observer or a camera, we need to first
apply the Lorenz contraction, and then, for every point on the object,
work out where it appears to be to the observer, given its current
velocity and position. The key equation turns out to be (hold onto your
sliderule:)
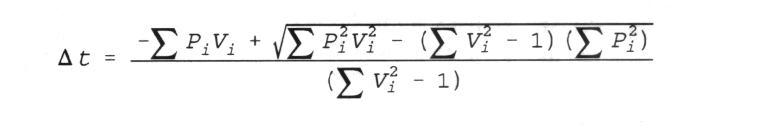 -Given the current position (Pi = Px, Py, Pz) of a particle, and
its velocity (Vi = Vx, Vy, Vz), this equation tells us how much time has
passed since the light we are seeing now left the particle. (i.e.
what the time difference in the observer's frame from the present, when
the observer sees light from the particle, and the event of that light
being emitted in the past.)
-Given the current position (Pi = Px, Py, Pz) of a particle, and
its velocity (Vi = Vx, Vy, Vz), this equation tells us how much time has
passed since the light we are seeing now left the particle. (i.e.
what the time difference in the observer's frame from the present, when
the observer sees light from the particle, and the event of that light
being emitted in the past.)
Knowing this, the apparent (visual) position of the point is simply:
Visual Pos = Actual_Pos - Delta_T * Velocity
(Where Delta_T is the quantity calculated above, the Actual_Pos is the current
position of the particle, and the velocity is the velocity of the particle.)
All Clear Now?
What it all Means
- Simply that with one equation we can tell, given a particle's current position
and velocity, where it appears to be. And since it's only one
equation it's quite easy to program into a computer, and get reasonably
swift animations out of it... However modelling
colour is a different story...
 Back to my home page
Back to my home page
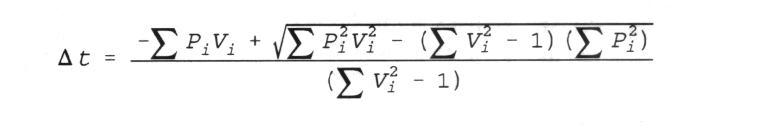 -Given the current position (Pi = Px, Py, Pz) of a particle, and
its velocity (Vi = Vx, Vy, Vz), this equation tells us how much time has
passed since the light we are seeing now left the particle. (i.e.
what the time difference in the observer's frame from the present, when
the observer sees light from the particle, and the event of that light
being emitted in the past.)
-Given the current position (Pi = Px, Py, Pz) of a particle, and
its velocity (Vi = Vx, Vy, Vz), this equation tells us how much time has
passed since the light we are seeing now left the particle. (i.e.
what the time difference in the observer's frame from the present, when
the observer sees light from the particle, and the event of that light
being emitted in the past.)